Accelerating Lightning Simulation with Neural Networks
In this post, we’ll look at how UNets can solve Laplace equations, which can be used to make lightning simulation faster.
Feel free to skip to the TL;DR section!
Dielectric Breakdown Model
As a part of my senior research project at UIUC, I worked to optimize a lightning simulation method called the dielectric breakdown model, or “DBM” for short. The DBM is a physics-based simulation. The method is broken down into two parts: shape generation and rendering. The shape generation is where the lightning pixels are chosen and it dominates the runtime. Shape generation works as follows:
- On a grid, add initial lightning pixel and ground pixels.
- Assign lightning pixels value 0, and ground pixels 1.
- Solve the Laplace equation $\nabla^2\phi = 0$
- A candidate is any empty pixel adjacent to an existing lightning pixel. Choose a new lightning pixel from the candidates randomly with a probability distribution given by the Laplace function. Specifically, choose a candidate with probability $p_i = \frac{(\phi_i)^\eta}{\sum_{j=1}^n (\phi_j)^\eta}$. $\eta$ is a parameter that controls the shape of the lightning.
- Go to step 2.
The slow part here is solving that Laplace equation for every lightning pixel. The fastest DBM lightning simulator uses an adaptive mesh method to solve it. It refines areas near lightning pixels, ground, and boundaries, and coarsens areas far away from those. It then runs a conjugate gradient solver on the mesh with some preconditioning that is very well suited for the lightning problem. This method is fast, but it runs on one CPU core.
Neural Network
It turns out that neural networks can solve the 2D Poisson equation for electric fields quite well. I trained a relatively small UNet on randomly generated lightning simulations to predict the Laplace equation solution for a given input image. Below is the UNet architecture.
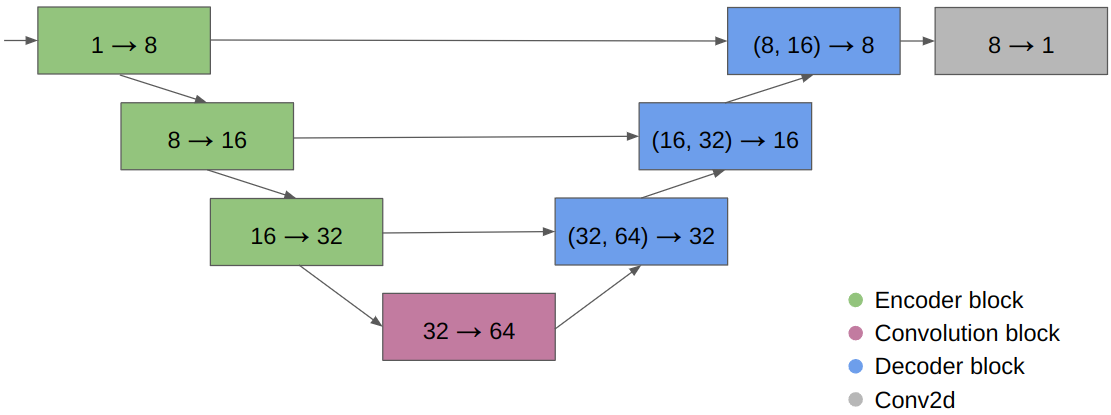
I trained the network with the Adam optimizer with a 0.001 learning rate and a mean square error loss over the candidate pixels. The neural net trains in about 11 minutes on an RTX 2060 on 90,000 samples. Below are the inputs and outputs on a validation set. For the map, white is lightning, red are candidates, and blue is ground. The input to our network is lightning pixels = -1, ground = 1, empty = 0.
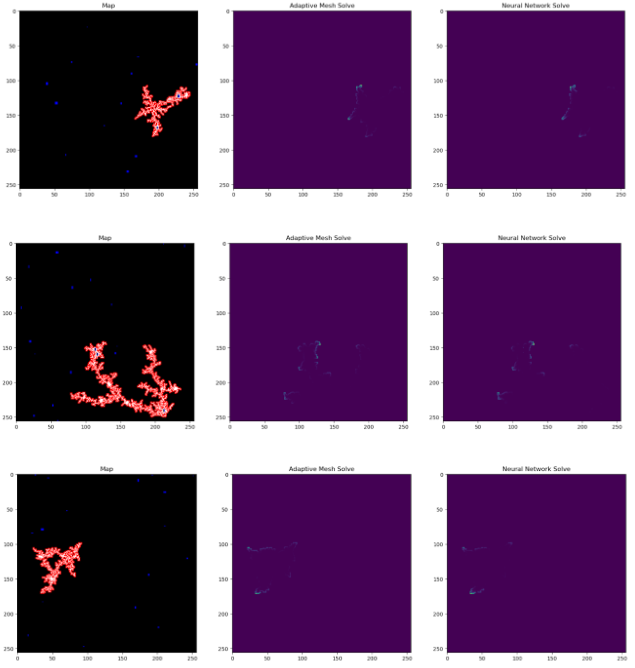
Results
The neural network method produces visually similar results at a fraction of the runtime! Because the UNet is a fully convolutional network, the neural network works for arbitrary square grid sizes with a side length that is a multiple of 32.

| Dimension | Average time per neural network Laplace solve (ms) | Average speedup compared to adaptive mesh |
|---|---|---|
| 256x256 | 1.40 | 4.64x |
| 512x512 | 4.71 | 5.82x |
| 1024x1024 | 19.1 | 13x |
The time taken to evaluate a neural network does not depend on the number of lightning pixels, unlike the adaptive mesh solver. This means speedups increase as the simulation grows. All benchmarks were run with a Ryzen 7 3800x, an RTX 2060, and 32GB of RAM.
Massively Parallel Simulations
Because our Laplace solve is dense, unlike the adaptive mesh, we can tile independent simulations together into one massive, super parallel simulation. As it turns out, in the absence of nearby ground, the probability for a candidate is dominated by nearby “noise” (attractive pixels added at random to the simulation according to blue noise). In practice, this means that we can reasonably simulate parts of the simulation independently and merge them back together as long as we choose an overlap that is at least twice the radius of the noise. For example, a 1024x1024 grid covered by 256x256 tiles with 64 pixel overlap:
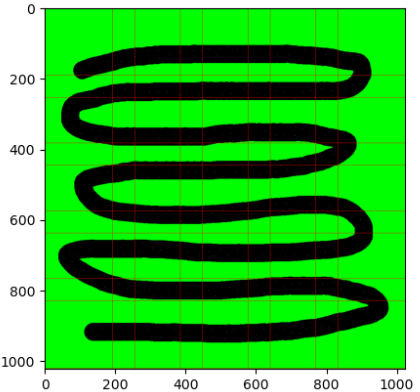
To blend the tiles together, we set a pixel value to be the weighted average of the tiles that contain it. The weight of a tile for a pixel is given by the square of a 2D gaussian centered at the tile’s center. This eliminates artifacts in the final Laplace solution. This technique also allows us to simulate lightning on non-square grids.
Conclusion
While this approach may yield too much error for scientific applications, it may still be useful in movies or video games. Could this approach be used as a warm start for other numerical methods? Could it be extended to 3D? I’ll be too busy graduating to find out for now :)
TL;DR
- The dielectric breakdown model is a physics-based lightning simulation method that requires solving a Laplace equation for every pixel of the lightning bolt
- The state of the art Laplace solver for this method is a sparse adaptive mesh solver which is fast, but runs on one CPU core
- Turns out neural networks can solve 2D Poisson equations for electric fields. A relatively small UNet can be trained on lightning simulations to estimate the Laplace equation solution for a given input image, running 4-13x faster than state of the art
- Since the neural net output is dense, it can be independently tiled to simulate lightning bolts at arbitrary resolutions massively in parallel