An Analysis of Poptropica's Mancala
This post analyzes Poptropica’s Mancala implementation and implements a perfect player you can play against online here. Give it a try! Source is here.
Background
Poptropica was a flash game I played in elementary school. Good times. I recently remembered a mancala minigame that I was never able to beat with my 10 year old prefrontal cortex:

I thought it could make for a fun project to write a computer strategy to destroy the opponent. I wanted to answer questions like: is the game solved? If so, who wins? What is the most elegant yet still efficient program we could write to play perfectly?
The result is a ~150 line C program that plays perfectly using alpha beta pruning and a transposition table. It can decide moves in < 1s running natively and something close to that when compiled to wasm and used in the interactive web version.
Game Rules
Poptropica’s board rules are standard Kalah(6, 3) rules with the “empty capture” rule. To summarize:
- The board has 6 “pits” on each side, each starting with 3 seeds. Hence (6, 3).
- If the last seed lands in the player’s store, the player goes again.
- If the last seed lands in an empty pit on the player’s side, move the seed and the seeds in the opponent’s opposite pit to the player’s store. The “empty capture” means you still do this even if there are no seeds in the opposite pit.
- If after any player’s turn, if any side is empty, the game immediately ends and seeds on each player’s side are sent to their respective stores.
Results
Standard Kalah(6, 3) is already solved as player 1 winning by 2. It’s the “empty capture” rule that sets Poptropica apart. However, even with the capture rule, we find that player 1 still wins by 2 under perfect play.
At one point I wrote a bug in the solver that ended the game when the current player had no moves rather than ending when either player had no moves. This caused the solution to be a draw instead of player 1 winning! I wonder if this means the game would be more fair under these rules? Or maybe with imperfect players, player 1 still has an advantage despite a theoretical draw. I’m not sure how to think about this.
Poptropica’s AI
I booted up Poptropica as an adult and headed over to the mancala minigame ready to get my revenge. I played it without any computer help and defeated the opponent soundly. Wait, what? What was the AI’s strategy? Why did I have any trouble with this as a kid?
I decompiled the .swf files and had a look at the AI’s strategy:
- 30% of the time, it chooses a random legal move.
- 70% of the time, it follows this decision process in order:
- Can it capture?
- Can it get another turn by landing in the store?
- Otherwise it plays the pit closest to their store.
If there are multiple ways to capture or get another turn, then it chooses the pit that’s closest to their store as the tie breaker. One thing to note is that the AI fails to consider wrap-around moves, like if their pit had 10 seeds, for example, which could cause the last seed to end up on their side again and potentially capture.
I was surprised to find that their AI doesn’t plan ahead at all. Compare that to the perfect playing bot that thinks 45+ turns ahead. I think I may have just been a dumb kid to lose here :)
Web UI
It was pretty anti-climactic to not need computer help to beat Poptropica’s AI. What am I going to use this solver for? I decided to hook the solver up to a web UI (Thanks Claude Code!) to bring Poptropica’s AI back to life in the way that I remembered it being as a kid: a perfect player.
It’s pretty fun to play against this thing for a time or two. I added an eval bar that you might see in chess, only that it tells you the future with absolute certainty, which I find hilarious:
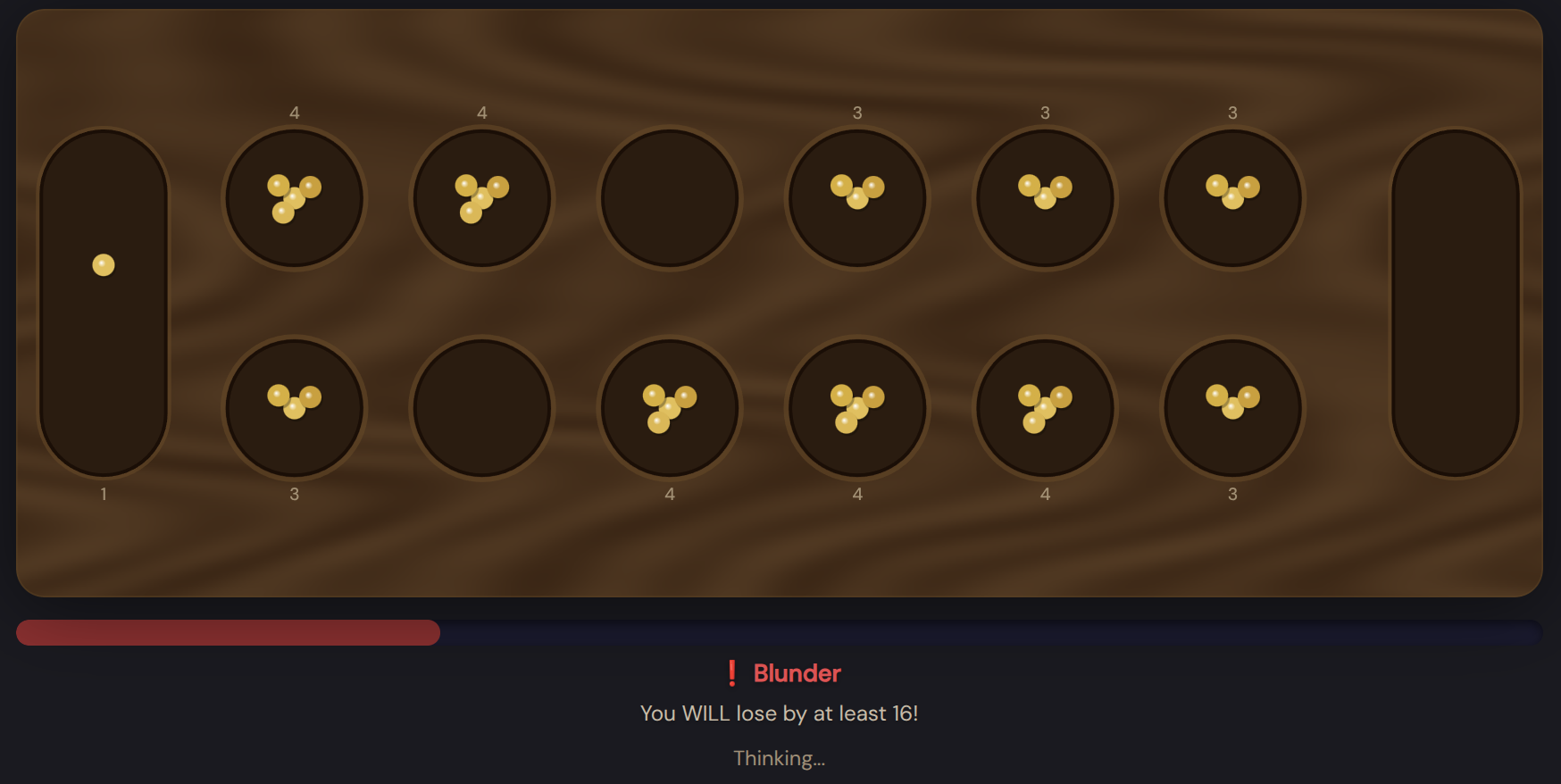
Enjoy!